Graphics can be a tricky topic, particularly when attempting to find anything on the internet these days that provides solution in terms of integer-only maths. embedded-graphics is a (mostly) integer-only library, so in pursuing a solution to good line joints for the Polyline and Polygon shape implementations, a bit of interweb detective work was required.

I eventually stumbled upon this StackOverflow question, the answers to which mostly seem to do what I'm looking for. I'm not a good mathematician by any means so the below code might not be stable in all situations, but it seems to work in a quick demo I whipped up.

I also posted the solution here on StackOverflow for posterity.

/// 2D integer point
struct Point {
    /// The x coordinate.
    pub x: i32,

    /// The y coordinate.
    pub y: i32,
}

/// Line primitive
struct Line {
    /// Start point
    pub start: Point,

    /// End point
    pub end: Point,
}

/// Check signs of two signed numbers
///
/// Fastest ASM output compared to other methods. See: https://godbolt.org/z/zVx9cD
fn same_signs(a: i32, b: i32) -> bool {
    a ^ b >= 0
}

/// Integer-only line segment intersection
///
/// If the point lies on both line segments, the second tuple argument will return `true`.
///
/// Inspired from https://stackoverflow.com/a/61485959/383609, which links to
/// https://webdocs.cs.ualberta.ca/~graphics/books/GraphicsGems/gemsii/xlines.c
fn intersection(l1: &Line, l2: &Line) -> Option<(Point, bool)> {
    let Point { x: x1, y: y1 } = l1.start;
    let Point { x: x2, y: y2 } = l1.end;
    let Point { x: x3, y: y3 } = l2.start;
    let Point { x: x4, y: y4 } = l2.end;

    // First line coefficients where "a1 x  +  b1 y  +  c1  =  0"
    let a1 = y2 - y1;
    let b1 = x1 - x2;
    let c1 = x2 * y1 - x1 * y2;

    // Second line coefficients
    let a2 = y4 - y3;
    let b2 = x3 - x4;
    let c2 = x4 * y3 - x3 * y4;

    let denom = a1 * b2 - a2 * b1;

    // Lines are colinear
    if denom == 0 {
        return None;
    }

    // Compute sign values
    let r3 = a1 * x3 + b1 * y3 + c1;
    let r4 = a1 * x4 + b1 * y4 + c1;

    // Sign values for second line
    let r1 = a2 * x1 + b2 * y1 + c2;
    let r2 = a2 * x2 + b2 * y2 + c2;

    // Flag denoting whether intersection point is on passed line segments. If this is false,
    // the intersection occurs somewhere along the two mathematical, infinite lines instead.
    //
    // Check signs of r3 and r4.  If both point 3 and point 4 lie on same side of line 1, the
    // line segments do not intersect.
    //
    // Check signs of r1 and r2.  If both point 1 and point 2 lie on same side of second line
    // segment, the line segments do not intersect.
    let is_on_segments = (r3 != 0 && r4 != 0 && same_signs(r3, r4))
        || (r1 != 0 && r2 != 0 && same_signs(r1, r2));

    // If we got here, line segments intersect. Compute intersection point using method similar
    // to that described here: http://paulbourke.net/geometry/pointlineplane/#i2l

    // The denom/2 is to get rounding instead of truncating. It is added or subtracted to the
    // numerator, depending upon the sign of the numerator.
    let offset = if denom < 0 { -denom / 2 } else { denom / 2 };

    let num = b1 * c2 - b2 * c1;
    let x = if num < 0 { num - offset } else { num + offset } / denom;

    let num = a2 * c1 - a1 * c2;
    let y = if num < 0 { num - offset } else { num + offset } / denom;

    Some((Point::new(x, y), is_on_segments))
}

In the demo, two line segments (red and green) are drawn. If they intersect and the point of intersection is on both line segments, a magenta dot is drawn at that point:

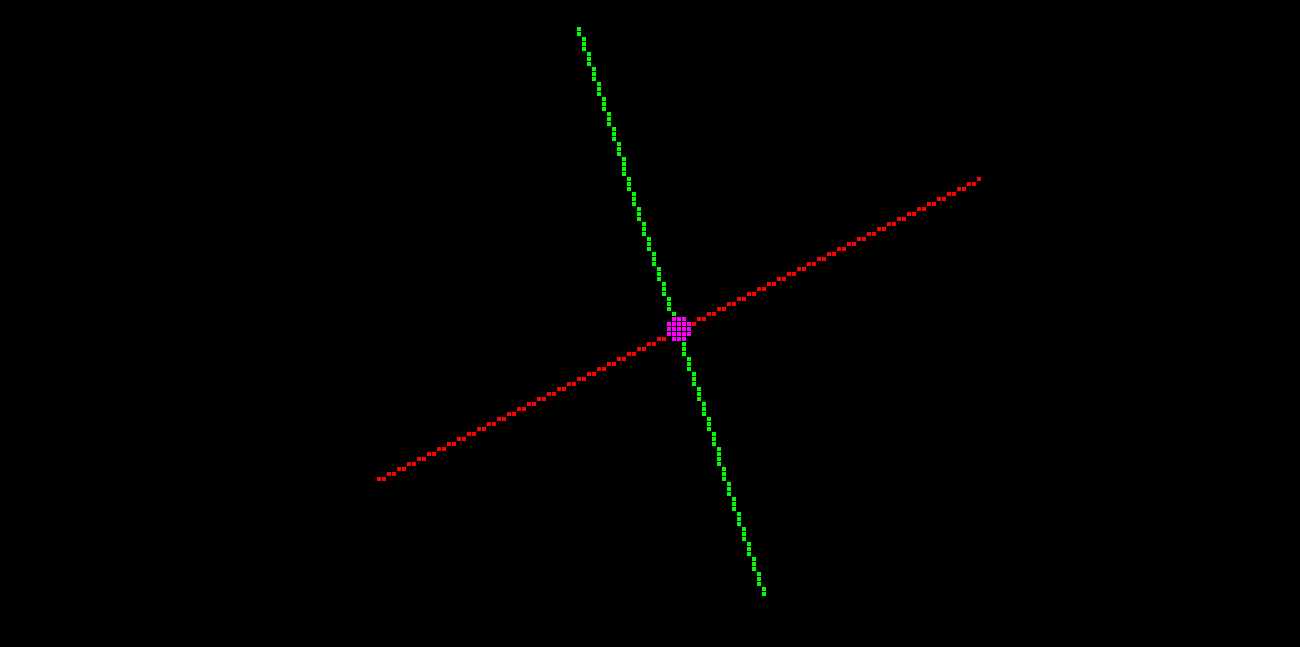
If the lines intersect, but the intersection does not lie on both line segments (i.e. the is_on_segments flag is false) , a cyan dot is drawn at the intersection:

.

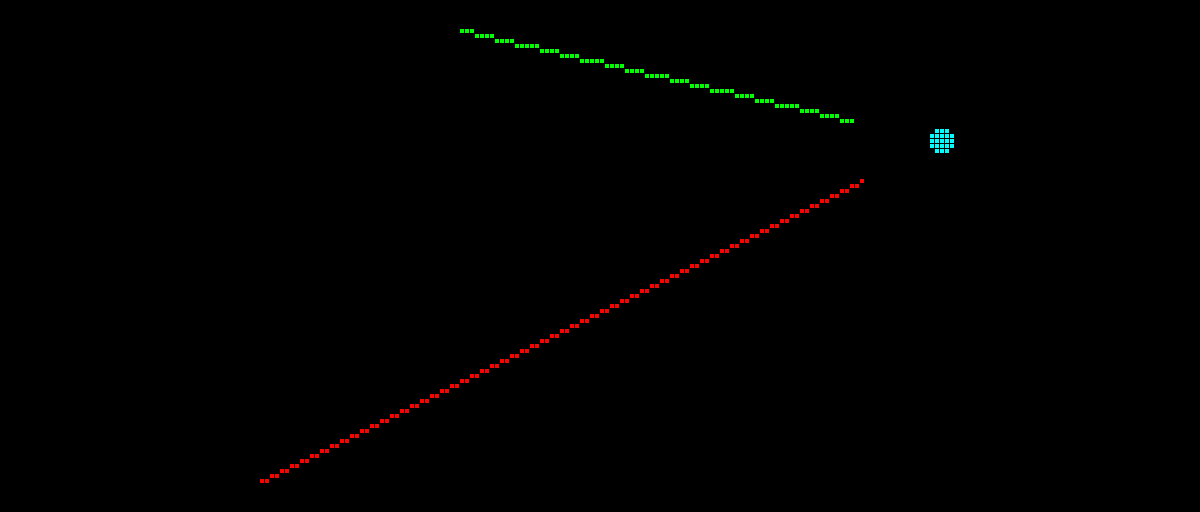Now that this is out of the way, I should be able to focus on getting thick line support for polylines, polygons and triangles working, as the above intersection logic is required to get "miter" style joints working correctly.